Révisions PARTIEL

Exercice 1

DM1 - Fourni par Mathys MACIA

Un sondage est réalisé auprès de 40 personnes pour connaître le nombre de livres qu’elles lisent par mois. Les résultats sont les suivants : $\{0,2,1,3,4,0,1,2,3,0,5,1,2,3,1,0,4,2,1,1,2,3,4,5,0,1,2,3,1,4,0,2,3,5,4,1,2,3,0,1\}$ Par convention, je décide de poser $\mathcal{E}=40$ qui représente l’effectif total de la série.

1. Déterminer la variable d’intérêt et son type. La variable d’intérêt est quantitative car elle représente une quantité, et on parle de variable quantitative discrète.

2. Construire le tableau des fréquences associées.

nombre de livre	0	1	2	3	4	5	TOTAL
effectif	7	10	8	7	5	3	40
fréquences	0.175	0.25	0.2	0.175	0.125	0.075	1

Rappel Soit $X$ une variable avec $(x_1,\dots ,x_n)$ les $n$ données et ${\mathcal{E}}_{total}$ l’effectif total de cette série (le nombre de données). Alors la fréquence notée $f_i$ de $x_i$ est donnée par : $f_i=\frac{{\mathcal{E}}_{x_i}}{{\mathcal{E}}_{total}}$ Où ${\mathcal{E}}_i$ représente l’effectif de $x_i$ .

Par exemple pour la fréquence des personnes qui ne lisent pas de livre notée $f_0$ où ${\mathcal{E}}_{x_0}=7$ et ${\mathcal{E}}_{total}=40$, on a alors :

$$f_0=\frac{7}{40}=0.175$$

On fait de même avec chaque autre effectif correspondant à chacune des possibilités.

3. Représenter graphiquement cette série. Puisque nous avons une variable de type quantitative alors nous allons la représenter à l’aide d’un diagramme bâton (diagramme barre). On souhaite représenter graphiquement cette série.

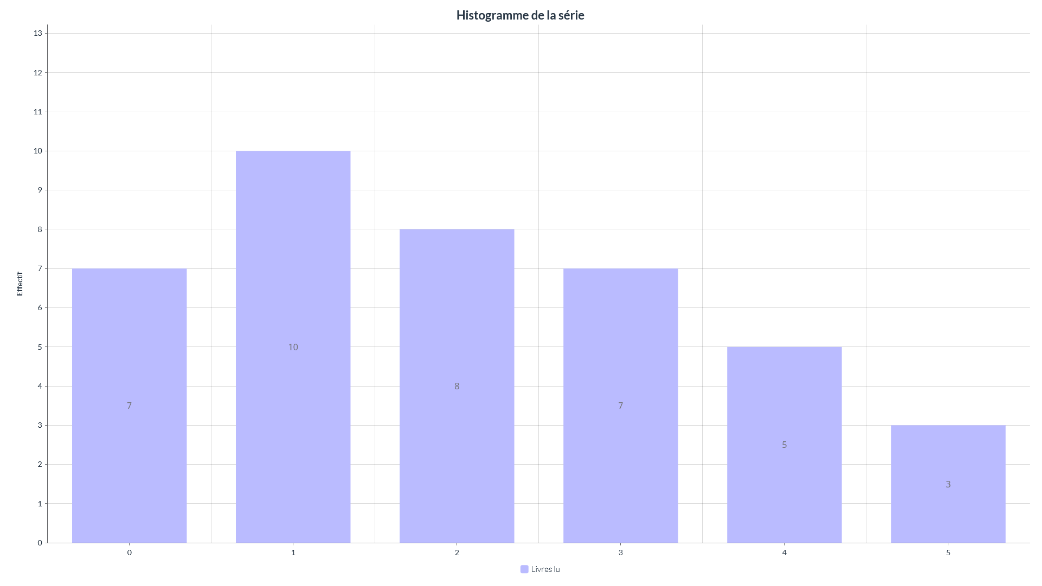
4. Calculer le nombre moyen de livre par mois. On chercher à calculer la moyenne de l’effectif.

==Rappel== Soit $X$ une variable avec $(x_1,\dots ,x_n)$ les $n$ données et ${\mathcal{E}}_{total}$ l’effectif total de cette série (le nombre de données). On note $\overline{x_n}$ la moyenne de la série définie par : $\overline{x_n}=\frac{\underset{i=1}{\sum ^n}{x}_i}{n}$

---

Point méthode Calculer la moyenne d’une série, un échantillon.

• On calcul la somme de toutes les données.
• On divise par le nombre de données

---

Ainsi, on a : $\underset{i=1}{\sum ^n}{x}_i=0\times 7+10\times 1+8\times 2+7\times 3+5\times 4+3\times 5=82$ d’où :

$$\overline{x_n}=\frac{\underset{i=1}{\sum ^n}{x}_i}{n}=\frac{82}{40}=2.05$$

La moyenne de livre lu par mois sur cette échantillon est de $2.05$ livres.

5. Déterminer la médiane et l’étendue de cette série. Calculons la médiane et l’étendue de cette série.

==Rappels==

• Soit $X$ une variable aléatoire avec $(x_1,\dots ,x_n)$ les $n$ données de l’échantilles (de la série). Alors l’étendue de la série notée $e$ est définie par : $e=x_{max}-x_{min}$

• Soit $X$ une variable aléatoire avec $(x_1,\dots ,x_n)$ les $n$ données de l’échantilles (de la série). Alors la médiane de la série est définie par : $med(X)=x_{\frac{n+1}{2}}\text{si }n\text{ est pair}$ >$med(X)=\frac{x_{(\frac{n}{2})}+x_{(\frac{n}{2}+1)}}{2}\text{si }n\text{ est impair}$

Ainsi, dans notre série on a :

• $x_{min}=0$
• $x_{max}=4$ d’où $e=4-0=4$ L’étendue de la série est donnée par $e=4$. Dans le même temps, on rappel que $n=40$. Ainsi : $med(X)=\frac{x_{\frac{40}{2}}+x_{\frac{40}{2}+1}}{2}=\frac{2+2}{2}=2$La médiane de cette série est donnée par $med(X)=2$.

6. Tracer la boîte à moustache de cette série.

---

Point méthode Tracer une boîte à moustache

• Déterminer les quartiles $q_1$, $q_2$ et $q_3$. En sachant que : $q_1=x_{25\%};q_2=med(X);q_3=x_{75\%}$
• Déterminer l’écart interquartile noté $Iq$ et défini par $Iq=q_3-q_1$
• Déterminer les bornes de votre boîte à moustache. J’ai décider de noter ces bornes $A$ et $B$. $A=q_1-1.5IqetB=q_3+1.5Iq$
  • Tracer votre boîte à moustache en respectant les bornes.
  • Tracer la position de la médiane à l’intérieur de votre boîte à moustache.
  • Placer (s’il y en a) les outliers (données hors de la boîte).

---

Ainsi, on a :

• $q_1=x_{25\%}=x_{0.25\times 40}=x_{10}=1$
• $q_3=x_{75\%}=x_{0.75\times 40}=x_{30}=3$
• $q_2=med(X)=2$ d’où
• $Iq=q_3-q_1=3-1=2$ Ainsi, je peux calculer les bornes de ma boîte à moustache.
• $A=q_1-1.5Iq=1-1.5\times 2=-2$ (on prendra à partir de $0$)
• $B=q_3+1.5Iq=3+1.5\times 2=6$ (on prendra la valeur max de notre série qui est $5$) On a alors toutes les informations pour tracer notre boîte à moustache. Tracé effectué avec le langage R

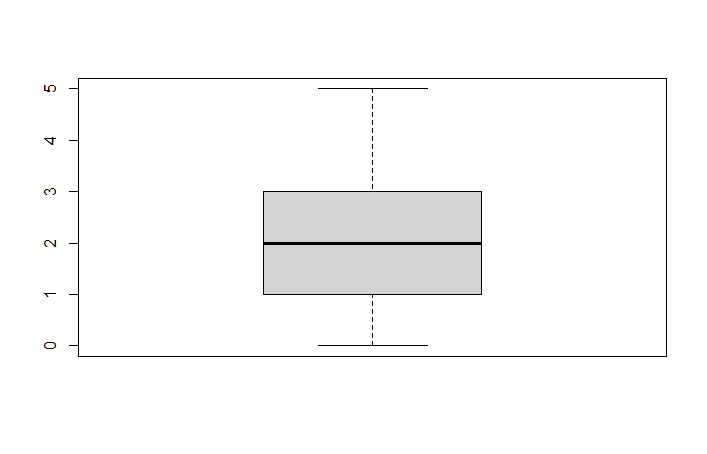
Exercice 2

DM1 - Fourni par Mathys Macia

On s’intéresse au relations entre la fréquence cardiaque au repos ($X$) et la pression artérielle moyenne $Y$ de $15$ patients. On a :

• $X=\{120,135,140,150,130,128,145,138,132,136,142,148,125,140\}$
• $Y=\{80,85,90,100,88,83,95,92,87,89,91,98,82,93\}$

Par convention, je note $n=15$ l’effectif total des séries de données.

1. Calculer les moyennes des fréquences cardiaques $X$ et des pressions artérielles moyennes $Y$. On a :

$$\overline{x_n}=\frac{120+135+140+150+130+128+145+\dots +148+125+140}{15}=127.26$$

et

$$\overline{y_n}=\frac{80+85+90+100+88+83+95+92+87+89+91+98+82+93}{15}=83.53$$

2. Calculer la variance et l’écart type des deux variables $X$ et $Y$.

==Rappel== Soit $X$ une variable associées à $n$ données alors, la variance notée $s_x^2$ est donnée par : $s_x^2=\frac{1}{n-1}\underset{i=1}{\sum ^n}(x_i-\overline{x_n})$ où $\overline{x}$ représente la moyenne de l’échantillon.

Calculons les variances une par une.

$$\begin{array}{rl}{s}_x^2& =\frac{1}{15-1}[(120-127.26{)}^2+(135-127.26{)}^2+\dots +(125-127.26{)}^2+(140-127.26{)}^2]\\ & =153.13\end{array}$$

et

$$\begin{array}{rl}{s}_y^2& =\frac{1}{15-1}[(80-83.53{)}^2+(85-83.53{)}^2+\dots +(93-83.53{)}^2]\\ & =67.8909\end{array}$$

==Rappel== Soit $X$ une variable associées à $n$ données alors, l’écart type notée $s_x$ est donnée par : $s_x=\sqrt{\frac{1}{n-1}\underset{i=1}{\sum ^n}(x_i-\overline{x_n})}=\sqrt{s_x^2}$ où $\overline{x}$ représente la moyenne de l’échantillon et $s_x^2$ la variance. Ainsi, l’écart type représente la racine carré de la variance.

Calculons l’écart type de chaque variable :

• $s_x=\sqrt{s_x^2}=\sqrt{153.13}=12.3745$
• $s_y=\sqrt{s_y^2}=\sqrt{67.8909}=8.2395$

3. Calculer la covariance entre $X$ et $Y$.

==Rappel== Soit $X$ une variable associées à $n$ données alors, la covariance notée $cov(X,Y)$ est donnée par : $s_{xy}=cov(X,Y)=\frac{\underset{i=1}{\sum ^n}(x_i-\overline{x_n})(y_i-\overline{y_n})}{n-1}$ où $\overline{x_n}$ et $\overline{y_n}$ représentent les moyennes respectives de chaque échantillons $X$ et $Y$.

Calculons cette covariance en respectant la formule donnée. On sait avec les questions précédentes que :

• $\overline{x_n}=127.26$
• $\overline{y_n}=83.53$
• $n=15$

---

Point méthode Calculer la covariance de deux échantillons

• Tracer la table des avec les colonnes suivantes
  • $X$
  • $Y$
  • ${\mathcal{E}}_1=(x_i-\overline{x_n})$
  • ${\mathcal{E}}_2=(y_i-\overline{y_n})$
  • ${\mathcal{E}}_1\times {\mathcal{E}}_2$
• Remplir les colonnes une à une
• Faire la somme des valeurs de la dernière colonne
• Diviser le tout par $n-1$

---

$X$	$Y$	${\mathcal{E}}_1=(x_i-\overline{x_n})$	${\mathcal{E}}_2=(y_i-\overline{y_n})$	${\mathcal{E}}_1\times {\mathcal{E}}_2$
120	80	-7.6	-3.53	26.828
125	85	-2.26	1.47	-3.3222
140	90	12.74	6.47	82.4278
150	100	22.74	16.47	374.5278
130	88	2.74	4.47	12.2478
128	83	0.74	-0.53	-0.3922
145	95	17.74	11.47	203.4778
138	92	10.74	8.47	90.9678
132	87	4.74	3.47	16.4478
136	89	8.74	5.47	47.8078
142	91	14.74	7.47	110.1078
148	98	20.74	14.47	300.1078
125	82	-2.26	-1.53	3.4578
140	93	12.74	9.57	121.9218
Ainsi, en ajoutant les éléments de la dernière colonne noté $c_4$, on a :
$\sum (c_4)=1386.6134$
d’où :
$s_{xy}=cov(X,Y)=\frac{\sum (c_4)}{n-1}=\frac{1386.6134}{15-1}=99.0438$
La covariance est donnée par $99.0438$.

4. Représenter le nuage de point et le barycentre sur le graphique.

==Rappel== Le barycentre représente le point noté $\mathcal{B}$ de coordonnées $(\overline{x_n},\overline{y_n})$.

Le nuage de point ainsi que le barycentre ont été générés avec le langage R. 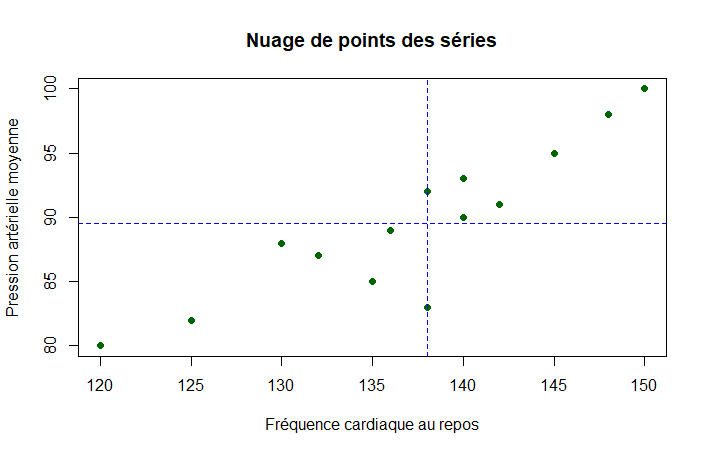Attention, le nuage de point n’est pas 100% correct, la série contient en fait 14 données et non 15, du coup ça fausse tout, mais comme j’ai la méthode et surtout la flemme de recommencer…

5. Proposer un modèle mathématiques pour expliquer la relation entre $X$ et $Y$. Nous allons utiliser un modèle linéaire de la forme : $Y={\beta }_0+{\beta }_{1}X$ pour expliquer la relation entre les deux variables. Où :

• ${\beta }_0$ représente le coefficient directeur de la droite
• ${\beta }_1$ représente l’ordonnée à l’origine

6. Utiliser la méthodes des moindres carrés pour estimer les coefficients de la régression linéaire.

---

Point méthode Utiliser et comprendre la méthode des moindres carrés

• Déterminer l’équation recherchée $Y={\beta }_0+{\beta }_{1}X$
• Déterminer les valeurs des coefficients $\widehat{{\beta }_0}$ et $\widehat{{\beta }_1}$ en sachant que : $\widehat{{\beta }_1}=\frac{s_{xy}}{s_x}et\widehat{{\beta }_0}=\overline{y_n}-\widehat{{\beta }_1}\overline{x_n}$ où :
  • $s_{xy}$ représente la covariance
  • $s_x$ l’écart type de $X$
  • $\overline{x_n}$ et $\overline{y_n}$ les moyennes des séries
• En déduire l’équation de la droite

---

En suivant à la lettre la méthode donnée juste au dessus, on chercher à déterminer l’équation de la droite $Y$. On vas commencer par déterminer $\widehat{{\beta }_1}$, en plus, on a déjà tout calculé précédemment. $\widehat{{\beta }_1}=\frac{s_{xy}}{s_x}=\frac{99.0438}{12.3745}=8.0038$ Ensuite, intéressons-nous à $\widehat{{\beta }_0}$, $\widehat{{\beta }_0}=\overline{y_n}-\widehat{{\beta }_1}\overline{x_n}=83.53-8.0038\times 127.26=-925.0335$

On ajoute un ”^” car ce sont des valeurs estimées.

7. Écrire l’équation de la droite de régression. Ainsi, d’après les résultats déterminés, on a : $Y=-925.0335+8.0038X$ Le coefficient directeur est ${\beta }_0=-925.0335$.

8. Calculer et interpréter les coefficients de corrélation et de détermination.

==Rappels== Soit $X$ une variable associées à $n$ données alors, on définit les coefficients de corrélation et de détermination comme suit :

• Coef. de corrélation ${\Omega }_{xy}=\frac{s_{xy}}{s_y}$
• Coef. de détermination $R^2=({\Omega }_{xy}{)}^2={\left(\frac{s_{xy}}{s_y}\right)}^2$ où $s_{xy}$ représente la covariance et $s_y$ l’écart type de $Y$.

Ainsi, d’après nos calculs précédents on a : ${\Omega }_{xy}=\frac{s_{xy}}{s_y}=\frac{99.0438}{8.2395}=12.0206$ et ainsi, $R^2=({\Omega }_{x,y}{)}^2=12.0206^2=144.4950$

Exercices du TD2

Exercice 1

Une entreprise emploie 500 personnes qui déjeunent à la cantine à l’un ou à l’autre des deux services avec une probabilité égale de manger au premier ou au second service. Si le gérant veut avoir une probabilité supérieure à $95\%$ de disposer d’assez de couverts, combien devra-t-il en prévoir pour chacun des deux services.

Avant de commencer à répondre aux questions Je récupère les informations importantes de l’exercice :

• effectif total $n=500$
• Notons $1$ le fait de “manger au premier service” et $0$ “manger au second service”. Ainsi, puisque les probabilités de manger à l’un ou à l’autre des service doivent être égales. Alors, chaque employé a $\frac{1}{2}$ chance de manger au premier ou au second service. On note alors $P(0)=P(1)=\frac{1}{2}$
• On cherche combien de couverts minimum le gérant doit-il disposer à chaque service pour en avoir assez. On notera ce nombre $k$.

1. On numérote les personnes par ordre alphabétique . On note $X_i$ la variable aléatoire valant $1$ si la $i\grave{e}me$ personne mange au premier service sinon $0$. Quelle est la loi de $X_i$ pour $1\le i\le 500$ ? Les deux possibilités le la loi $X_i$ peuvent être vu comme un échec ou une victoire, ainsi $X_i$ suit une loi de Bernoulli de paramètre $P$. On note : $X_i⇝Ber(P)$ Et lorsque l’on a récupéré les infos, on a défini la loi qui dit que : $P(X_i=0)=\underset{P(X_i=1)}{\underbrace{1-P(X_i=0)}}=\frac{1}{2}$ Ainsi on a : $X_i⇝Ber\left(\frac{1}{2}\right)$

2. On suppose que les variables aléatoires $X_i$ sont indépendantes pour $1\le i\le 500$. Quelle est la loi exacte de la variable aléatoire $S_n=\underset{i=1}{\sum ^{500}}{X}_i$ L’hypothèse de la question dit que chaque variable $X_i$ sont indépendantes, cela semble raisonnable dans le cas d’une numérotation par ordre alphabétique. On rappel que l’on chercher le nombre minimum $k$ de couverts à positionner à chaque services. Ici, dans notre cas, $S_n$ représente le nombre de personnes qui mangent au premier service. On note alors : $P(X_i=1)=S_n$ Si $S_n$ détermine le nombre de personnes qui mangent au premier service, alors le restant mangeront au second service, on note alors : $P(X_i=0)=500-S_n$ Ainsi on chercher le nombre minimum de couverts $k$ à disposer à chaque service, pour être certain de disposer d’assez de couverts à chaque service. C’est à dire : $S_n\le ket500-S_n\le k$ La loi exacte de la variable aléatoire $X_i$ est alors donnée par : $P(S_n\le ket500-S_n\le k)\ge 0.95$ La loi de $S_n$ est une loi binomiale $\mathcal{B}(\underset{effectif}{\underbrace{n}},\underset{proba}{\underbrace{p}})=\mathcal{B}(500,\frac{1}{2}$).

3. Calculer $E(S_n)$ et $Var(S_n)$.

==Rappel==

• $E(S_n)$ représente l’espérance.
• $Var(S_n)$ représente la variance. Puisque $S_n$ suit une loi binomiale tel que $X_i⇝\mathcal{B}(n,p)$ alors on a : $E(S_n)=n\times petVar(S_n)=npq=np(1-p)$ où $q$ représente la probabilité “d’échec”, autrement dit $q=1-p$.

Ainsi, en utilisant le rappel fourni on a : $E(S_n)=500\times \frac{1}{2}=250etVar(S_n)=500\times \frac{1}{2}\times (1-\frac{1}{2})=125$ 4. Que représente la variable aléatoire $(500-S_n)$ dans le contexte ? Comme évoquée précédemment, la variable aléatoire notée $(500-S_n)$ représente en fait le nombre de personnes qui mangent au second service.

5. Par quelle loi peut-on approcher la loi de $S_n$ ? Préciser ses paramètres. On utilise une loi normale de paramètres : $S_n^{\ast }⇝\mathcal{N}(\mu ,{\sigma }^2)=\mathcal{N}(E(S_n),Var(S_n))=\mathcal{N}(250,125)$ On peut approcher cette loi à l’aider d’un loi normale centrée et réduite.

==Rappel== Lorsque l’on souhaite centrer et réduire une loi normale, alors pour une variable $X$ tel que $X⇝\mathcal{N}(\mu ,{\sigma }^2)$ Pour centrer et réduire, afin de suivre une loi normale de paramètre $0$ et $1$, on a : $\frac{X-\mu }{\sqrt{{\sigma }^2}}⇝\mathcal{N}(0,1)$

Que l’on vas noter $S_n^{\ast }$ défini par : $S_n^{\ast }=\frac{S_n-250}{\sqrt{125}}⇝\mathcal{N}(0,1)$

6. Déterminer le paramètre $k$. On rappel que l’on cherche : $P(S_n\le ket500-S_n\le k)\ge 0.95$ On a :

• $500-S_n\le k⟺S_n\ge 500-k$ Ainsi on obtient alors

$$P(500-k\le S_n\le k)\ge 0.95$$

Ce qui donne en centrant et réduisant, en fin de compte :

$$P\left(\frac{500-k-250}{\sqrt{125}}\le S_n^{\ast }\le \frac{k-250}{\sqrt{125}}\right)=P\left(\frac{250-k}{\sqrt{125}}\le S_n^{\ast }\le \frac{k-250}{\sqrt{125}}\right)$$

où :$\frac{S_n-250}{\sqrt{125}}⇝\mathcal{N}(0,1)$ En négligeant les erreurs d’approximation on cherche $k$ minium tel que : $\varphi \left(\frac{250-k}{\sqrt{125}}\right)-\varphi \left(\frac{k-250}{\sqrt{125}}\right)\ge 0.95$

==Rappel== $-\varphi (x)=\varphi (x)-1$

Ainsi grâce au rappel effectué on a : $2\varphi \left(\frac{250-k}{\sqrt{125}}\right)-1\ge 0.95⟺\varphi \left(\frac{250-k}{\sqrt{125}}\right)=\frac{0.95+1}{2}=0.975$ Ainsi on a :$\varphi \left(\frac{250-k}{\sqrt{125}}\right)=0.975$ Par lecture des quantiles de la loi normale, on a $\varphi (1.96)=0.975$. Ainsi on a : $k\ge 250+1.96\times \sqrt{125}⟺k\ge 271.91$

7. Interpréter la valeur de $k$ dans le contexte. Ainsi, puisque $k\ge 271.91$ pour que le gérant soit certain d’avoir assez de couverts pour les deux services à 95%, il doit placer au moins 272 couverts à chaque services.

Exercice 2

TO DO…