Cours - AlgoProg4

Algorithmique & Programmation 4

C’est quoi un algorithme ?

Définition

On appelle algorithme une suite finie d’instructions précises et ordonnées qui permettent de résoudre un problème, d’accomplir une tâche. Les algorithme sont une base de la programmation informatique et sont utilisés pour automatiser des processus complexes.

Caractéristiques d’un algorithme

• FINITUDE, il doit se terminer après un nombre fini d’étapes.
• PRÉCISION, chaque étape doit être clairement définie (= sans ambiguïté)
• ÉFFICACITÉ, il doit être optimisé :
  • en terme de temps d’exécution
  • en terme d’utilisation de ressources
• ENTRÉE, il peut recevoir une ou plusieurs entrées
• SORTIE, il produit au moins un résultat

De manière schématique un algorithme peut être vu comme :

$$entr\acute{e}e⟼proc\acute{e}dure⟼sortie$$

Introduction du cours

Un algorithme correct à 90% n’est pas correct.

Nous nous sommes demandés si il est possible de prouver qu’un algorithme est correct. Kurt Gödel (logicien et mathématicien Autrichien) a démontré qu’aucun système formel suffisamment puissant pour décrire l’arithmétique ne peut prouver sa propre cohérence au sein de ce même système. En France (mais pas que), il existe un courant de recherche qui construit des programmes basés sur des algorithmes pour prouver des algorithmes. Par exemple l’assistant de preuve Coq. Si l’on fait un algorithme “soigné”, alors en théorie, il n’y a pas de problèmes pour que le programme le soit lui aussi. Malgré tout cela n’est pas toujours vrai, par contre avoir des bonnes bases est important pour faire un bon programme.

Définition

Le terme efficacité d'un algorithme c’est se demander si mon programme me donne une réponse dans un temps raisonnable.

Attention

• L’efficacité d’un algorithme et l’efficacité d’un programme ne représente pas la même chose.
• L’efficacité d’un algorithme prend en compte la puissance d’un ordinateur, alors il faut prendre en compte plusieurs systèmes, afin de tester l’algorithme plusieurs fois indépendamment du système choisit.

Définition

On appelle programme informatique un algorithme qui a été codé sur machine à l’aide d’un langage spécifique.

Efficacité d’un algorithme

Si l’on dit l’algorithme $\mathcal{A}$ s’exécute en $10s$ ceci n’a pas de sens, comme on l’a expliqué au dessus, l’efficacité dépend de la machine. Ainsi, lorsque l’on étudie l’efficacité d’un algorithme on doit répondre à plusieurs questions :

• Sur quelle machine ?
• Pour quelle(s) entrée(s) On considère que l’efficacité d’un algorithme se mesure grâce aux opérations que l’algorithme fait. Pour déterminer l’efficacité de ce dernier on va en fait calculer le nombre d’opérations effectuées.

Exemple : On considère l’algorithme $A_1$ suivant.

Entree :
	T un tableau de N entiers
Sortie :
	L'entier minimum du tableau T

Algorithme A
	m <- T[1]
	pour i allant de 2 à N
	faire
		Si m > T[i]
		alors
			m <- T[i]
		fin si
	fin pour
	retourner m
fin A

On va voir que l’efficacité sera mesurée en fonction de N. Voici ce que fait le programme :

• il associe à m le premier élément du tableau
• Il parcours les le tableau à partir du $2-\grave{e}me$ élément jusqu’au N-ième donc l’algorithme boucle N-1 fois
• Il compare deux entiers pour savoir lequel est plus petit
  • Si vrai : Affectations
  • Si faux : Rien
• Retourne m

Attention

En algorithmique le premier élément d’un tableau, d’une liste est l’élément d’indice 1 !

Étudions différents cas de figure possible

1. Si N=10 et T trié dans l’ordre croissant
   • $1$ affectation (au début de l’algo)
   • N-1=9 tour de boucles donc $9$ comparaisons Dans le cas d’un tableau T trié dans l’ordre croissant, le premier élément est forcément le premier élément du tableau, alors la condition m>T[i] est toujours fausse ce qui implique que l’on ne réaffecte aucunes valeurs à m, elle garde la même valeur tout le temps de l’algo.
   • $1$ retour
   • $10$ contrôles

Remarque

L’opération controle c’est le nombre de fois qu’on vérifie si i inférieur ou égal à N. En gros notre boucle dans l’algo elle vas de 2->N, ainsi pendant l’exécution la variable i prend les valeurs suivantes :

$$i:2\to 3\to 4\to \dots \to N\to N+1$$

Vous allez me dire pourquoi $N+1$ et bien parce que on prend i inférieur ou égal à N, du coup si i=N le tour de boucle vas se faire. Mais lorsque i prend la valeur N+1 c’est à ce moment là que la boucle pour se stoppe. C’est pour cette raison qu’il y a à chaque fois N comparaisons.

2. Si N=10 et T trié dans l’ordre décroissant

   • $1$ affectation (au début de l’algo)
   • N-1=9 tour de boucles, donc $9$ comparaisons Puisque le tableau T est trié dans l’ordre décroissant alors le plus petit élément du tableau se trouve forcément en fin de tableau, ainsi à chaque tout on réaffecte la valeur courante T[i] à m. On compte alors $9$ affectations supplémentaires
   • $1$ retour
   • $10$ contrôles Ainsi ici on a 10 affectations et 10 contrôles.

3. Si N=1000 et T trié dans l’ordre croissant

   • $1$ affectation (au début de l’algo)
   • 1000-1=999 tout de boucles donc $999$ comparaisons Tableau trié dans l’ordre croissant donc premier élément forcément le plus petit m représente déjà le minimum dès la première affectation.
   • $1000$ contrôles

Si on résume globalement ce que l’on apperçoit

• Comparaisons : N-1
• Nombre de contrôles : N
• Nombre de retours : 1
• Nombre d’affectations : Meilleure cas 1 (dans l’ordre croissant) Pire cas N (dans l’ordre décroissant)

Ainsi, on en conclu que le nombre d’affectation dépend de l’entrée même si l’entier N n’est pas fixé.

Comment avancer dans l’analyse algorithmique ?

Définitions

• On appelle opération élémentaire une action de base généralement exécutée en un temps constant selon la machine. Elles permettent d’évaluer la complexité d’un algorithme.
• Les opérations arithmétiques $+,-,\ast ,/,DIV,MOD$
  • $DIV$ pour déterminer le quotient d’une division euclidienne
  • $MOD$ pour déterminer le reste d’une division euclidienne
• Les comparaisons ==, <=, >=, <, >, != (sur des types élémentaires)
• Les opérateurs logiques
  • ET OU qui prennent 2 booléens
  • NON qui prend 1 booléen
• Les opérations de contrôles permettent de gérer les boucles, les conditionnelles, le résultat

Dans nos études, nous considérerons que la taille de l’entier est minimale, même si cette dernière dépend du codage.

Remarque

Si on fixe une base $b$ et un nombre $N$, alors on aura pour chiffre de $N$ :

$$N=\lceil {\log }_b(N)\rceil$$

Pour rappel Soit $x\in \mathbb{R}$ alors on note sa valeur entière supérieure par $\lceil x\rceil$.

Exemple : Pour $N=14$,

• en base $10$ $N$ possède deux chiffres
• en base $2$ on a $N=1110$ ($2^3+2^2+2^1$)
• en codage unitaire on a $11111111111111$

Remarque

2 logs sont égaux à une constante près.

Exemple : Si on prend $1000$ entiers codés sur $4$ octets on aura alors $4000$ octets utilisés. Pour $N$ entiers on aurait $4\times N$, c’est une fonction linéaire.

$$taille=N\times tailleCodage$$

Définition

On appelle ordre de grandeur la tendance d’une courbe quand $N$ augmente.

En algorithmique, L’ordre de grandeur est utilisée pour évaluer la tendance du temps d’exécution (ou de l’espace mémoire) requis par un algorithme en fonction de la taille donnée. Cela permet en fait de classer les algorithmes selon leur efficacité sans se soucier des constantes ou des termes qui influent peu. L’ordre de grandeur est notée $O$, avec la notation Big-O qui donne une approximation asymptotique de la complexité.

Dans ce cours, on utilisera la notation de Landau $\mathcal{O}$ créée par Brechmann en 1894 et popularisée par Landau, qui permet de décrire le comportement des fonctions selon la tendance de $N$, pour objectif de déterminer la complexité de certains algorithmes.

Dans l’objectif de mieux comprendre la notation $\mathcal{O}$ de Landau, nous allons utiliser quelques exemples.

Rappel

Dans le cadre des Maths pour l’info en L1 La notion de suite/fonction dominée a été introduite. Soient $f$ et $g$ deux fonctions, on dit que $f$ est dominée par $g$ si et seulement si :

$$\exists C>0\mid \forall n_0\ge nf\le C(f)$$

En français, on cherche un rang $n_0$ à partir duquel $f$ est plus petit ou égal à $g$.

Exercice

• On considère $g(n)=3n^2+5n+10$ une fonction et on veut montrer que $g\in \mathcal{O}(n^2)$.
• On considère $h(n)=9n+5$ montrer que $h=\mathcal{O}(n)$.

Correction

Pour plus de facilité nous allons prendre chaque termes de la fonction et étudier leur signe par rapport à $n^2$.

$$\begin{array}{rlr}3n^2& \le 3n^2& \forall n\ge 0\\ 5n& \le n^2& \forall n\ge 5\\ 10& \le n^2& \forall n\ge 4\end{array}$$

Ainsi si je regroupe les trois inégalités et que je prend le rang $n_0$ qui permet de respecter les conditions, j’obtient :

$$3n^2+5n+10\le 5n^2\forall n\ge 5$$

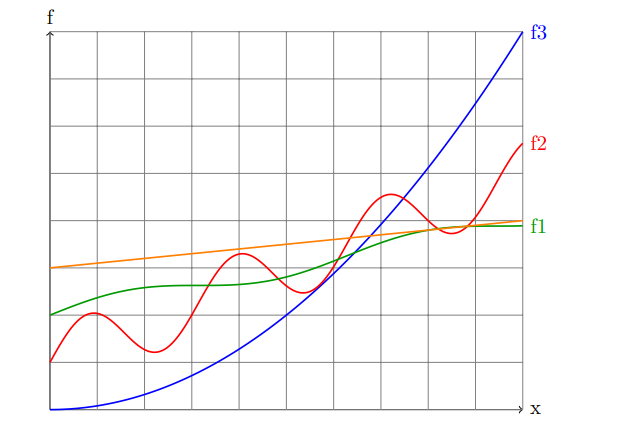En reprenant les fonctions données par M.Sanlaville pendant les CMs, étudions asymptotiquement les allures des courbes $f_1$, $f_2$ et $f_3$.

• Pour $f_1$ La courbe verte semble croire lentement avec peu d’oscillation, son comportement est semblable à $g(x)=x$ ou $g(x)=log(x)$
• Pour $f_2$ La courbe rouge semble croire plus vite que $f_1$ mais présente plus d’oscillations. En la lissant on peut définir qu’elle suit une tendance semblable à $g(x)=x$.
• Pour $f_3$ La courbe bleue semble croitre plus rapidement que les deux autres, de manière exponentielle ou quadratique. On a $g(x)=x^2$ par exemple.

Propriétés

• Soit $g$ une fonction alors on a $g=\mathcal{O}(g)$ Une fonction $g$ se domine elle même.
• Soit $f$ et $g$ deux fonctions :

$$(f=\Theta (g))⟺(f=\mathcal{O}(g)\wedge g=\mathcal{O}(f))$$

En gros, si $f=\Theta (g)$ ça revient à dire que $f$ et $g$ croient de manière proportionnelle, qu’elles ont la même complexité asymptotiques.

Complexité des algorithmes

Définitions

• On appelle complexité au pire d’un algorithme $\mathcal{A}$ la fonction qui permet de donner le nombre maximum d’opérations élémentaire qu’effectue un algorithme en fonction de $N$ la taille de l’entrée. Généralement on ne donne pas une fonction exacte mais plutôt un ordre de grandeur
• À l’inverse, on appelle complexité au mieux d’un algorithme $\mathcal{A}$ la fonction qui permet de donner le nombre minimum d’opérations élémentaire que fais cet algorithme en fonction de $N$.
• La complexité en moyenne est plus hypothétique, on connais la probabilité des entrées, on cherche la fonction qui donne le nombre moyen d’opérations élémentaire.

Pour la complexité d’une boucle pour à $p$ itérations et $k$ (constant) opérations élémentaire On va avoir une complexité en $\mathcal{O}(nk)$ mais, puisque $k$ est une constante, on peut la négliger et on se retrouve dans le pire, le meilleure des cas et en moyenne à $\mathcal{O}(n)$.

Exemple : On considère les boucles suivantes :

pour i = 1 -> N-1
	pour j = 0 -> N-i
		Comparer T[j], T[j+1]
			peut être changer j, j+1

Dans notre cas :

• On dispose de deux boucles, une sur i et une sur j.
• On a deux opérations élémentaires constantes Comparer échanger

En regardant les boucles de plus près :

• Boucle externe De i allant de 1 à N-1 on boucle donc N-1 fois dans tous les cas
• Boucle interne De i allant de 0 à n-i Puisque i démarre à 0, alors on ajoute obligatoirement un tour de boucle supplémentaires quelque soit N Ainsi, on bouclera N-i+1 fois pour toutes les possibilités de N Ainsi, le nombre d’opérations élémentaires de la boucle interne est donnée par :

$$S_n=\underset{i=1}{\sum ^{N-i}}(N-i+1)\times k$$

• $k$ constante, le nombre d’OE
• La somme $S_n$ regroupe toutes les comparaisons effectuées pendant l’exécution de l’algorithme En gros le nombre d’opérations de la boucle interne c’est la somme du nombre d’itérations de cette dernière en fonction de i multiplié par le nombre d’OE.

Remarque

Dans la suite l’acronyme OE signifie opération élémentaire.

Complexité du tri à bulle

Le tri à bulle (ou bubble sort) est un algorithme de tri permettant de trier progressivement les éléments d’un tableau en échangeant les éléments adjacents pour les placer progressivement dans le bonne ordre. Le principe

• Compare les éléments adjacents
• Si deux éléments sont pas dans le bon ordre il sont échangés
• Après chaque passage, l’élément le plus “grand” se retrouve en fin de tableau

Algorithme du tri à bulle

Fonction tri_a_bulle(T)
    n ← longueur(tableau)
    Pour i allant de 0 à n - 1
        Pour j allant de 0 à n - i
            Si T[j] > T[j + 1] alors
                Échanger T[j] et T[j + 1]
            Fin Si
        Fin Pour
    Fin Pour
Fin Fonction

Ainsi, la complexité du tri à bulle est la suivante :

$$C(n)=\underset{i=1}{\sum ^{N-1}}(N-i+1)\times k=\left(\underset{i=1}{\sum ^{N-1}}N-\underset{i=1}{\sum ^{N-1}}i+\underset{i=1}{\sum ^{N-1}}1\right)\times k$$

On décompose les sommes pour que ce soit plus simple :

$$\underset{i=1}{\sum ^{N-1}}N=N\times \underset{i=1}{\sum ^{N-1}}1=N(N-1)=\mathcal{O}(N)$$ $$\underset{i=1}{\sum ^{N-1}}i=\frac{N(N-1)}{2}=\mathcal{O}(N^2)\text{ a savoir !}$$ $$\underset{i=1}{\sum ^{N-1}}1=N-1=\mathcal{O}(N)$$

Ainsi on se retrouve avec :

$$C(n)=\mathcal{O}(N^2)-\mathcal{O}(N)+\mathcal{O}(N^2)=\mathcal{O}(N^2)$$

Propriétés des sommes

Propriétés sur les sommes

à retenir sur les sommes, connu depuis algèbre de base… en ajoutant les aspects drôles de l’algorithmique et des complexités

$$\underset{i=1}{\sum ^N}k=k\times N=\mathcal{O}(N)$$

Propriétés sur les sommes

$$\underset{i=1}{\sum ^N}ik=k\times \underset{i=1}{\sum ^N}i=k\times \frac{N(N+1)}{2}=\mathcal{O}(N^2)$$

Propriétés sur les sommes

$$\begin{array}{rl}\sum _{i=1}^{N-1}(N-i)k& =k\times \sum _{i=1}^{N-1}(N-i)\\ & =k\times \left(\sum _{i=1}^{N-1}N-\sum _{i=1}^{N-1}i\right)\\ & =k\times \left(N(N-1)-\frac{N(N-1)}{2}\right)\\ & =k\times \left(\frac{2N(N-1)-N(N-1)}{2}\right)\\ & =k\times \left(\frac{N(N-1)}{2}\right)\\ & =\mathcal{O}(N^2)\end{array}$$

Propriété sur les sommes

$$\begin{array}{rl}\sum _{i=1}^N\sum _{i=1}^{N}k& =\sum _{i=1}^{N}1\times \sum _{i=1}^{N}1\times k\\ & =N\times N\times k\\ & =\mathcal{O}(N^2+k)=\mathcal{O}(N^2)\end{array}$$

Exemple : On considère le code suivant :

pour i allant de 1 à N
	pour j allant de 1 à N
		pour k allant de 1 à N
			// Instructions constantes OE

On a alors une complexité définie par :

$$\underset{i=1}{\sum ^N}\underset{i=1}{\sum ^N}\underset{i=1}{\sum ^N}k=\mathcal{O}(N^3+k)=\mathcal{O}(N^3)$$

Pour une boucle TANT QUE

tant que <condition>
faire
	// k opérations élémentaires, k = Cste

Rappel

On note Cste une constante.

Alors, le code suivant possède une complexité au pire. Il faut alors trouver $k_{max}$, le nombre d’opérations élémentaires maximum.

$$C_{pire}=\Theta (k_{max})$$

Algorithme récursif

Définition

Un algorithme récursif est une méthode permettant de ressourdre des problèmes en s’appelant elle-même, afin de résoudre des sous-problèmes du même type. généralement la récursivité est utilisé pour des problèmes qui veut être divisés en sous-problèmes similaires. Un algorithme récursif nécessite :

• Une condition d’arrêt, en gros c’est le moment ou l’algorithme arrête de s’appeler lui-même (sinon récursion infinie)
• Appel récursif

Pour mieux comprendre la notion de récursivité prenons un exemple concret

Recherche dichotomique

L’algorithme de recherche dichotomique (ou recherche binaire) est un algorithme efficace permettant de rechercher un élément dans un tableau trié. Il repose sur le principe des méthodes “diviser pour régner” en réduisant l’espace de recherche de moitié à chaque étape. Principe de base :

• On choisit un x recherché
• On se place au milieu du tableau T trié
• On récupère m l’élément au milieu du tableau
  1. x=m on arrête de chercher, on a trouvé.
  2. x<m alors puisque le tableau est trié tous les éléments après m seront plus grands, alors on réeffectue la recherche sur la moitié gauche.
  3. x>m On réeffectue la recherche sur la moitié droite.
• Si les indices se croisent, ou si on a trouvé x, on s’arrête.

Algorithme de la recherche dichotomique

Entrees :
	D la liste d'élément trié
	x l'élément cherché
	deb l'indice de début de la partie de tableau
	fin l'indice de fin de la partie du tableau
Sortie :
	indice de l'élément x si trouvé

Algorithme rechDico
	SI debut > fin
	ALORS
		RETOURNER -1
        
    milieu <- (debut + fin) DIV 2
    elemMiddle <- D[milieu]
    
    SI elemMiddle = x 
    ALORS
        RETOURNER milieu // Mot trouvé, retourne sa position
    SINON SI x < elemMiddle 
    ALORS
        rechDico(D, x, deb, millieu-1) // Chercher dans la moitié gauche
    SINON
        rechDico(D, x, millieu+1, fin) // Chercher dans la moitié droite
    FIN SI
fin algo

Dans cette algorithme, pour déterminer la complexité on compte le nombre d'OE (hors appels récursifs ) qui déterminera le nombre d’appels. Ici, la complexité ne sera pas la même selon les cas

• Dans le meilleur des cas L’élément est pile au milieu du tableau alors on a $\Theta (1)$

• En moyenne, on ne peut pas déterminer car on a pas d’informations sur la taille des l’entrées ou autre

• Dans le pire des cas L’élément est sois le tout premier élément soit le tout dernier alors la méthode vas se faire sur des parties de tableau divisées de moitié à chaque appel récursif jusqu’à ce qu’il ne reste qu’un élément à comparer. Autrement dit le nombre d’opérations va être :

  $$N\to \frac{N}{2}\to \frac{N}{4}\to \frac{N}{8}\to \dots \to 1⟺log(N)$$

  Ainsi dans le pire des cas la complexité de la recherche dichotomique est donnée par $\Theta (log(N))$.

Avec un nombre d’opérations élémentaires qui suit une fonction $f(n)$ avec $N$ la taille de l’entrée, alors la complexité sera donnée par $NbAppels\times f(N)$. Le nombre d’opération peut dépendre aussi de la taille des données traitées par appel.

Exemple : Taille des données par appel récursif : $N$ puis $N-1$ puis $N-2$, … respectivement de taille $T_1$, $T_2$, $\dots$. Et $f(T_i)=k\times T_i$ (linéaire).

Alors la complexité au pire, lorsque l’on fait tous les appels de $1$ à $N$ est donnée par :

$$C=\underset{i=1}{\sum ^N}k\times T_i=k\times \underset{i=1}{\sum ^N}{T}_i=k\times \frac{N(N+1)}{2}=\Theta (N^2)$$

On peut aussi avoir le cas où il y a 2 appels un appel sur une taille Ti qui à l’intérieur contient deux appels T{i+1} et T{i+1}'.

Un exemple trop vu : Fibonacci

La suite de Fibonacci est définie par :

$$u_0=u_1=1\forall n\ge 2,u_n=u_{n-1}+u_{n-2}$$

Ainsi on obtient l’algorithme récursif suivant :

Entree :
	N le rang de la suite
Sortie :
	Le terme de rang n de la suite de fibo

Algorithme fibo
	SI N=0 OU N=1
	ALORS
		RETOURNER 1
	SINON
		RETOURNER fibo(n-1)+fibo(n-2)
	FIN SI
FIN Algo

Alors, pour un appel au rang N on peut avoir deux appels qui sont sur N-1 pis N-2.

ARBRE D’APPELS DE LA SUITE DE FIBONACCI 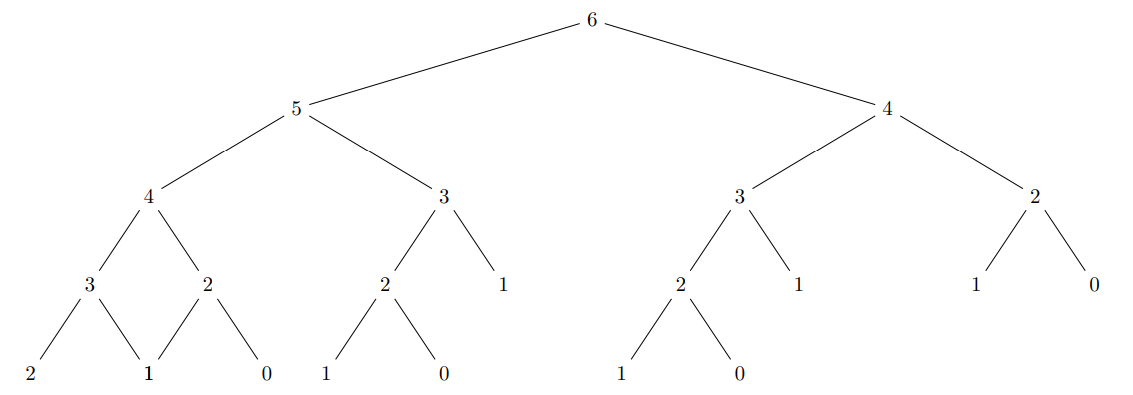On voit que :

• Pour N=6 on fait 23 appels
• Pour N=5 on fait 13 appels
• Pour N=4 on fait 8 appels On peut déduire que le nombre d’appels est exponentiel lorsque N devient grand.

En général :

$$T_{i+1}et{T}_{i+1}^{\prime }\sim \frac{T_i}{2}$$

Si on coupe l’ensemble des données en $a$ parties de taille $\frac{n}{b}$ alors :

$$C(n)=a\times C\left(\frac{n}{b}\right)+f(n)$$

où $f(n)$ représente le nombre d’OE à l’intérieur de l’appel.

• Au départ : N=n
• À la fin : N=Cste ou condition validée

Attention

Les formules suivantes s’appliquent uniquement aux algorithmes où la relation de récurrence est de la forme :

$$C(n)=a\times C\left(\frac{n}{b}\right)+f(n)$$

où :

• $a$ représente le nombre de sous-problèmes
• $b$ le facteur de réduction de taille
• $f(n)$ le coût des opérations

Théorème maître (Master Theorem)

1. Si $f(n)=\Theta (n^{{\log }_{b}a-ϵ})$ pour $ϵ>0$
   Dans ce cas, la fonction $f$ croit plus lentement que ${\log }_{b}a-ϵ$, donc le coût total est dominé par le temps de résolution des sous-problèmes.
   Alors $C(n)=\Theta (n^{{\log }_{b}a})$
2. Si $f(n)=\Theta (n^{{\log }_{b}a})$
   Alors $C(n)=\Theta (n^{{\log }_b(a)}\times \log (n))$
   Le coût des sous problèmes sont du même ordre.
3. Si $f(n)=\Omega (n^{{\log }_{b}a+ϵ})$ avec $ϵ>0$
   Alors $C(n)=\Theta (f(n))$
   Dans ce cas $f(n)$ croît plus vite que le coût des sous-problèmes donc $f$ domine.

Si $a=b$ alors $lo{g}_b=1$
Alors on dispose de 3 cas différents

• $f(n)=\Theta (n^{1-ϵ})$ donc $\Theta (n)$
• $f(n)=\Theta (n)$ donc $\Theta (n\times \log (n))$
• $f(n)=\Omega (n^{1+ϵ})$ donc $\Theta (f(n))$

Dans le cas de la recherche dichotomique, c’est le second cas. On prend alors $a=1$ et $b=2$, $f(n)$ qui est une constante pour la formule générale. On se retrouve avec le cas : $C(n)=\Theta (\log (n))$.

Notion de finitude d’un algorithme

La première chose demandée à un algorithme, c’est de terminer son exécution en un temps fini. Ce n’est pas évident pour un algorithme. Considérons une boucle tant que (boucle for : nbBoucle fixé à l’avance), en supposant que le nombre d’OEdans la boucle est bornée.

Définition

On appelle variant noté $V$ pour une boucle $B$ une quantité entière, bornée et strictement décroissante à chaque itération de $B$.

Rappel

Le terme borné signifie que le variant est compris dans un intervalle, qu’il existe un nombre plus petit ou égal (minoré) et un nombre plus grand ou égal (majoré).

Pour montrer qu’un algorithme est fini (= terminaison) il faut analyser s’il comporte un nombre fini d’étapes et s’il s’arrête après un temps fini pour toutes les entrées possibles.

Définition

On dit d’un algorithme qu’il est fini s’il se termine après un nombre fini d’étapes, quelque soit l’entrée choisie.

Objectif

• Identifier un variant qui décroit à chaque itération
• Vérifier l’absence de boucle infinies
• S’assurer que chaque “branches” de l’algo mène à une terminaison

Considérons l’algorithme suivant

var D <- LT - LA
TANT QUE D > 0
FAIRE
	LA <- LA+D
	LT <- LT + D/2
	D <- LT-LA
FIN TANT QUE
RETOURNER (LA)

Quelques précisions :

• Les entrées
  • LA, LT deux réels, dans notre exemple considérons que LA=0 et LT=100
• Sortie
  • LA un réel Les variables LA et LD représente nt respectivement la longueur d’Achille et la longueur de la tortue et D la distance entre eux. Sauf que puisque LT>LA, alors la distance ne sera jamais inférieur ou nul alors, Achille ne rattrapera jamais la tortue. Hors, si on programme cet algorithme en JAVA par exemple, il se termine, sinon il est infini en théorie.

Exemple 01 : Prenons en compte l’algorithme de recherche du plus grand diviseur commun par l’algorithme d’Eulcide.

Entree :
	x, y deux entiers
Sortie :
	x le pgcd(x, y)

Algorithme PGCD
	a <- x
	b <- y
	SI a<b
	ALORS
		echanger a et b
	FIN SI
	TANT QUE b > 0
	FAIRE
		(q, r) <- divEuclidienne(a, b)
		a <- b
		b <- r
	FIN TANT QUE
	RETOURNER a
FIN Algo

• À chaque tour de boucle, on a $b$ prend la valeur du reste de la division euclidienne de $a$ par $b$.
• b diminue strictement à chaque itération car r<b par définition
• Donc b diminue strictement à chaque itération
• b est un entier et est borné inférieurement par $0$ Dans notre cas, le variant $V=b$.

Ainsi :

• à chaque itération $b$ diminue d’au moins $1$
• comme $b$ est initialement un entier fini et qu’il ne peut pas être nul ou plus petit, la boucle se terminera après un certain nombre fini de tour
• Lorsque $b=0$, la boucle s’arrête et le programme renvoie $a$ Ces trois aspects prouvent la finitude de mon algorithme, $b$ décroit à chaque itération, a une borne inférieure $0$ et une borne supérieur $max(x,y)$, et prend valeurs initiale dans un ensemble ordonnée, les entiers naturels.

Exemple 02 : Considérons un autre algorithme, celui de la puissance de $2$. Qui permet de déterminer si l’entier passé en paramètre est pair.

Entree :
	x l'entier a tester
Sortie :
	pair le booleen qui défini si x est pair

Algo puissanceDeux
	m <- x
	pair <- VRAI
	TANT QUE (m>1) et PAIR
	FAIRE
		pair <- m est pair
		m <- m DIV 2
	FIN TANT QUE
RETOURNER PAIR
FIN Algo

Ici, cherchons le variant. On remarque vite que :

• m est borné inférieurement par $1$
• m est borné supérieurement par x
• m DIV 2 implique que m décroit de moitié à chaque itération Ainsi ici, notre variant est donné par $V=m$. D’où puisque $V=m$, que m est bornée, diminue à chaque itération, la boucle tant que s’arrêtera après un nombre fini d’opérations, et lorsqu’elle se termine l’algorithme renverra pair. Ainsi nous venons de montrer la finitude de l’algorithme puissanceDeux.

Notion de correction d’un algorithme

La correction d’un algorithme désigne la propriété selon laquelle un algorithme produit systématiquement le résultat attendu. Autrement dit, un algorithme est dit correct lorsqu’il fournit toujours une solution correcte pour toute les entrées valides.

Définitions

• On dit qu’un algorithme est partiellement correct si il fourni un résultat correct lorsqu’il finit forcément par se terminer (= finitude). Mais, cette notion de garantit pas toujours que l’algorithme se termine.
• On dit qu’un algorithme $\mathcal{A}$ est totalement correct quand il est à la fois partiellement correct et qu’il termine pour toutes les entrées possibles. Autrement dit un algorithme est correct lorsqu’il se finit et fournit des sorties valides pour toutes entrées valides.

Méthode pour montrer la correction Vérifier la correction d’un algorithme peut se faire de plusieurs façons

1. Preuve par induction (utilisé pour des algorithmes récursifs/itératifs)
   • Montrer que l’algorithme fonctionne correctement pour un cas de base.
   • Supposer qu’il fonctionne pour un cas arbitraire $n$
   • Démontrer qu’il fonctionne pour le cas suivant $n+1$ Raisonnement par récurrence
2. Invariant de boucle (algorithmes itératifs)
   • Identifier une propriété qui est vraie avant, pendant et après chaque itération de la boucle.

Considérons un algorithme $\mathcal{A}$ avec :

• Entrée : $e\in D_e$
  Un algorithme qui prend en entrée des éléments de l’ensemble $D_e$.
• Sortie : $s\in D_s$
  Une algorithme qui renvoie un résultat $s$ qui appartient à un ensemble $D_s$.
• Variable : Y
  Variable interne utilisée par l’algorithme pendant l’exécution. On note :
• $\varphi (e)$ un prédicat vérifié pour tout $e\in D_e$.
  On parle de PRÉCONDITION.
• $\psi (e,s)$ un prédicat vérifiant si la sortie $s$ produit par l’algorithme est correcte pour l’entrée $e$.
  On parle de POSTCONDITION.

On dit que l’algorithme $\mathcal{A}$ est correct si :

1. Il se termine (finitude)
2. $\psi (e,s)$ est vraie pour tout couple entrée sortie

Reprenons l’exemple précédant L’algorithme ici que l’on vas nommer $puissance$ permet de vérifier si un entier x passé en paramètre est une puissance de $2$.

Entree :
	x l'entier a tester
Sortie :
	pair le booleen qui défini si x est pair

Algo puissanceDeux
	m <- x
	pair <- VRAI
	TANT QUE (m>1) et PAIR
	FAIRE
		pair <- m est pair
		m <- m DIV 2
	FIN TANT QUE
RETOURNER PAIR
FIN Algo

Si on récupère les informations à disposition :

• Les entrées possibles sont des $x\in \mathbb{N}$ (= entiers naturels)
• La sortie est un booléen permettant de dire si x est une puissance de $2$

Étapes de l’algorithme :

• On associe à la variable m la valeur de x.
• pair est initialiser à VRAI car on suppose que x est une puissance de 2.
• La boucle TANT QUE boucle lorsque :
  • m>1 (on a pas encore atteint la valeur 1)
  • pair est encore VRAI les divisions précédentes ont permis de maintenir la parité de m.
• Corps de la boucle TANT QUE
  • par est VRAI si m est pair
  • m est divisé par 2
• On retourne la valeur finale de pair

Analyse de l’algorithme Pourquoi cet algorithme fonctionne t-il ? Par définition un entier $x$ est une puissance de $2$ si : Il est positif strict Il peut être divisé plusieurs fois par $2$ jusqu’à obtenir $1$ sans jamais devenir impair lors des divisions successives.

Pour $x=8$ alors on a :

$$8\to 4\to 2\to 1$$

On s’arrête car on a attend $1$, $x=8$ est donc une puissance de $2$. Pour $x=12$ on a :

$$12\to 6\to 3$$

On s’arrête car $3$ est impair, ainsi $12$ n’est pas une puissance de $2$.

Preuve de la correction

• Précondition : L’entier en paramètre doit être strictement positif, on note

  $$\varphi (x)=x\in {\mathbb{N}}^{\ast }$$

• Postcondition : L’algorithme retourne VRAI si et seulement si $x$ est une puissance de $2$. On note

  $$\psi (x,pair):pair=(\exists k\in \mathbb{N}\mid x=2^k)$$

Correction partielle

• Initialisation
  Au départ pair=VRAI et m=x
• Invariant de boucle
  À chaque itération de la boucle TANT QUE, si pair reste VRAI, alors tous les m précédant sont pairs, ce qui est nécessaire pour qu’un nombre soit une puissance de $2$.
• Terminaison
  La boucle TANT QUE se termine lorsque m=1 ou lorsque pair devient Faux (une division par $2$) produit un nombre impaire.
  On note V=m le variant car il décroit à chaque tour de boucle d’au moins $1$, alors il y aura forcément un moment ou soit m=1 ou m<1 dans ce cas la boucle s’arrête et l’algorithme renvoi la valeur de pair.
• Conclusion
  Si l’algorithme se termine avec pair=VRAI alors x sera forcément une puissance de $2$.

Correction totale

• La variable m est divisée par 2 à chaque itération, donc elle décroit strictement et atteindra forcément $1$ ou une valeur inférieure à $1$, assurant la fin de la boucle TANT QUE.

Cherchons la formule de l’invariant

Définition

On appelle invariant une propriété qui reste vraie tout le long de l’exécution d’une boucle ou d’un programme, à chaque itération.

Reprenons la boucle TANT QUE

TANT QUE (m>1) et PAIR
FAIRE
	pair <- m est pair
	m <- m DIV 2
FIN TANT QUE

Alors on a :

• m la variable divisée par 2 à chaque itération
• k Un compteur représentant le nombre d’itération effectuées.
• On note reste la valeur qui représente le reste des divisions précédentes.
  • Vaut $1$ si m devient impaire après une division
  • Sinon $0$

Ainsi on a :

• $x=2^k$ avec $k\in \mathbb{N}$ si c’est une puissance de $x$ On obtient alors l’invariant suivant :

$$I=m\times 2^k+reste\times 2^{k-1}$$

Essayons de montrer ce dernier par récurrence.

• Initialisation au début de l’algorithme On a m=x, k=0 et reste=0 Donc :

  $$I=m\times 2^0+reste\times 2^{-1}=x\times 1+0\times 0.5=x$$

  L’invariant $I$ déterminé est vrai pour l’initialisation.

• Récurrence On suppose que $I$ est vrai pour $k\in \mathbb{N}$ itérations, montrons que cela se maintient pour $k+1$ itérations. On a :

$$\begin{array}{rl}I& =m_{k+1}\times 2^{k+1}+rest{e}_{k+1}\times 2^{k-1+1}\\ & =m_{k+1}\times 2^{k+1}+rest{e}_{k+1}\times 2^k\end{array}$$

Au rang $k$, je sais que $I=m_k\times 2^k+rest{e}_k\times 2^{k-1}$, alors lorsque l’on divise $m_k$ pour l’itération suivante, on obtient :

$$m_k=2\times m_{k+1}+rest{e}_{k+1}$$

d’où on se retrouve avec :

$$\begin{array}{rl}I& =(2\times m_{k+1}+rest{e}_{k+1})\times 2^k+rest{e}_k\times 2^{k-1}\\ & =\underset{\text{partie entieˋre quotient iteˊration k+1}}{\underbrace{m_{k+1}\times 2^{k+1}}}+\underset{\text{reste des divisions par 2 de toutes les iteˊrations confondues}}{\underbrace{\underset{\text{reste division iteˊration k+1}}{\underbrace{rest{e}_{k+1}\times 2^k}}+\underset{\text{reste division aˋ l’iteˊration k}}{\underbrace{rest{e}_k\times 2^{k-1}}}}}\end{array}$$

Ainsi au terme $k+1$ on retrouve le quotient et le reste de la division de l’itération ainsi que le reste de la division précédente. La structure de l’invariant est globalement respectée à chaque itération.

Exemple supplémentaire : On considère l’algorithme $maximum$ qui permet de rechercher le maximum dans une liste de nombre.

Entree :
	Tableau T de nombres
Sortie :
	Element le plus grand du tableau T

Algorithme maximum
	max <- T[1]
	POUR i = 2 à N
	ALORS
		SI T[i]>max
			max <- T[I]
		FIN SI
	FIN POUR
	RETOURNER max
FIN maximum

On peut noter T = [t1, t2, ..., tn] le tableau.
Dans l’objectif de prouver la correction de l’algorithme, il faut trouver un invariant de boucle.

Rappel

Un invariant $I$ de boucle $B$ représente une propriété qui est vrai avant, pendant (chaque itération) et après (sortie) uen boucle.

Soit $i$ un entier strictement positif, on note $\varphi (i)$ la propriété “max = maximum([t1, t2, ..., ti])”. En gros, $i$ représente la taille de l’entrée, le nombre d’éléments du tableau.

• Initialisation :
  Pour $i=1$, alors le tableau T ne contiendra qu’un seul élément. Si on exécute l’algorithme, avant de rentrer dans la boucle, le minimum est le premier élément du tableau T[1], ainsi la propriété est vraie AVANT LA BOUCLE.
• Hérédité :
  Supposons que $\varphi$ soit vraie au début de l’itération $i$,, c’est à dire que max = maximum([t1, ..., ti]), montrons que me résultat sera conservé après itération de la boucle. On cherche à montrer que : max = maximum([t1, ..., ti, ti+1]). On a à l’itération $i$, max = maximum([t1, ..., ti])

    SI T[i]>max
    	max <- T[I]
    FIN SI
  

  • Si T[i+1] <= max alors sa valeur ne change pas selon la condition IF de l’algorithme
  • Si T[i]>max alors la valeur du maximum prend comme nouvelle valeur T[i] qui est donc la plus grande valeur du tableau
    Ainsi, dans les deux cas présentés ici, la valeur du maximum du tableau est conservée, $\varphi$ reste vraie à chaque itération.
• Conclusion :
  L’invariant reste vrai après la dernière itération de la boucle, d’indice i. On peut noter alors que le résultat de l’itération i-1 et i restent les mêmes pour un tableau de i éléments :

max = maximum([t1, ..., ti-1]) = max = maximum([t1, ..., ti)

On vient donc grâce à l’invariant de montrer la correction partielle de cette algorithme. Pour terminer, l’algorithme possède une boucle for qui se termine après un nombre connu d’itérations. Ainsi l’algorithme est fini. En somme :

• $maximum$ est fini
• $maximum$ respecte bien une propriété avant, après chaque itérations et à la sortie de la boucle.

Remarque

Ainsi pour montrer la correction il faut :

• Prouver que l’algorithme est fini
  • En utilisant un variant $V$
• Déterminer un invariant $I$ et démontrer par récurrence que ce dernier est vrai avant la boucle, pendant chaque itération, et à la sortie de la boucle.

Compléments

• Correction examen 2024 : Correction de l’examen AP4 2024