Exercice 1
Une entreprise emploie 500 personnes qui déjeunent à la cantine à l’un ou à l’autre des deux services avec une probabilité égale de manger au premier ou au second service. Si le gérant veut avoir une probabilité supérieure à de disposer d’assez de couverts, combien devra-t-il en prévoir pour chacun des deux services.
Avant de commencer à répondre aux questions Je récupère les informations importantes de l’exercice :
- effectif total
- Notons le fait de “manger au premier service” et “manger au second service”. Ainsi, puisque les probabilités de manger à l’un ou à l’autre des service doivent être égales. Alors, chaque employé a chance de manger au premier ou au second service. On note alors
- On cherche combien de couverts minimum le gérant doit-il disposer à chaque service pour en avoir assez. On notera ce nombre .
-
On numérote les personnes par ordre alphabétique . On note la variable aléatoire valant si la personne mange au premier service sinon . Quelle est la loi de pour ? Les deux possibilités le la loi peuvent être vu comme un échec ou une victoire, ainsi suit une loi de Bernoulli de paramètre . On note : Et lorsque l’on a récupéré les infos, on a défini la loi qui dit que : Ainsi on a :
-
On suppose que les variables aléatoires sont indépendantes pour . Quelle est la loi exacte de la variable aléatoire L’hypothèse de la question dit que chaque variable sont indépendantes, cela semble raisonnable dans le cas d’une numérotation par ordre alphabétique. On rappel que l’on chercher le nombre minimum de couverts à positionner à chaque services. Ici, dans notre cas, représente le nombre de personnes qui mangent au premier service. On note alors : Si détermine le nombre de personnes qui mangent au premier service, alors le restant mangeront au second service, on note alors : Ainsi on chercher le nombre minimum de couverts à disposer à chaque service, pour être certain de disposer d’assez de couverts à chaque service. C’est à dire : La loi exacte de la variable aléatoire est alors donnée par : La loi de est une loi binomiale ).
-
Calculer et .
Rappel
- représente l’espérance.
- représente la variance. Puisque suit une loi binomiale tel que alors on a : où représente la probabilité “d’échec”, autrement dit .
Ainsi, en utilisant le rappel fourni on a : 4. Que représente la variable aléatoire dans le contexte ? Comme évoquée précédemment, la variable aléatoire notée représente en fait le nombre de personnes qui mangent au second service.
- Par quelle loi peut-on approcher la loi de ? Préciser ses paramètres. On utilise une loi normale de paramètres : On peut approcher cette loi à l’aider d’un loi normale centrée et réduite.
Rappel Lorsque l’on souhaite centrer et réduire une loi normale, alors pour une variable tel que Pour centrer et réduire, afin de suivre une loi normale de paramètre et , on a :
Que l’on vas noter défini par :
- Déterminer le paramètre . On rappel que l’on cherche : On a :
- Ainsi on obtient alors
Ce qui donne en centrant et réduisant, en fin de compte :
où : En négligeant les erreurs d’approximation on cherche minium tel que :
==Rappel==
Ainsi grâce au rappel effectué on a : Ainsi on a : Par lecture des quantiles de la loi normale, on a . Ainsi on a :
- Interpréter la valeur de dans le contexte. Ainsi, puisque pour que le gérant soit certain d’avoir assez de couverts pour les deux services à 95%, il doit placer au moins 272 couverts à chaque services.
Exercice 2
Soit une variable aléatoire de loi gaussienne centrée et réduite et un nombre réel strictement positif fixé.
Avant de commencer l’exercice Je récupère les infos importante.
- suit une loi gaussienne centrée et réduite .
- un réel strictement positif. .
-
Représenter sur un graphique et faire apparaître la loi de . Puisque alors on peut représenter graphiquement la densité de la loi gaussienne centrée et réduite.
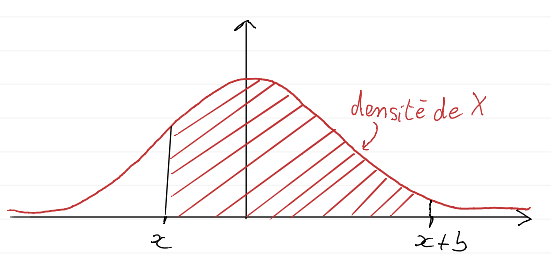 Puisque suit une loi gaussienne centrée et réduite alors elle est de paramètres . Admet une densité de la forme :
Ici, puisque suit une loi gaussienne centrée et réduite alors :
On note
Ainsi on a :
Où représente la fonction de répartition de .
Puisque suit une loi gaussienne centrée et réduite alors elle est de paramètres . Admet une densité de la forme :
Ici, puisque suit une loi gaussienne centrée et réduite alors :
On note
Ainsi on a :
Où représente la fonction de répartition de . -
Déterminer tel que soit maximum. On cherche tel que . C’est à dire :
Ce qui revient à dire que . En gros on a :
On a alors d’après la seconde ligne : d’où . Donc .
- Exprimer cette probabilité maximum en fonction de la fonction de répartition de . Pour quelle valeur de est-elle égale à ? Ainsi, on a :
On cherche donc tel que :
Par lecture de la table de la loi normale centrée et réduite on a d’où .
Exercice 3
Lire sur la table du Khi-deux. Soit une variable aléatoire distribuée selon une loi du Khi-deux .
-
Déterminer la valeur de solution de l’équation pour . On a . Puisque , on peut directement lire la table Et on trouve alors .
-
Déterminer la valeur de solution de l’équation pour . On a . Puisque alors, on ne peux pas lire directement sur la table. Je vais alors calculer Ainsi je lit la table case . Et on trouve alors .
-
**Déterminer la valeur de solution de l’équation pour X \leadsto \mathcal{X}(15)X \leq x1-P=1-0.9=0.1(0.1, 15)x=22.307$.
Point méthode Déterminer la solution d’une équation avec la table de Khi-deux. Soit une variable aléatoire qui suit une loi de Khi-deux de paramètre .
- Pour .
- Je lis la table et
- Pour
- Je calcul
- Je lis la table à et
Exercice 4
Lire sur la table de Student Soit une variable aléatoire distribuée qui suit une loi de Student .
-
Déterminer la valeur solution de l’équation , pour . On a et . Je sais que ainsi on lit la table à la ligne et à la colonne . On obtient .
-
Déterminer la valeur solution de l’équation , pour . On a et . Je sais que , mais je suis dans le cas alors la table me donnera , ce sera à moi d’inverser le signe pour trouver mon inconnue. En lisant la table à la ligne et à la colonne , On obtient .
-
Déterminer la valeur solution de l’équation , pour . On a et . Je sais que , Or alors, à la place du de départ on vas prendre . On recommence avec :
- et . Alors, on sait que . On lit la table à la ligne et à la colonne . Ainsi on obtient .
Point méthode Déterminer la solution d’une équation avec la table de Student. Soit une variable aléatoire qui suit une loi de Student de paramètre .
- Pour .
- Je détermine
- Je lis la table à la et
- Pour
- Je détermine
- Je détermine avec la table à la et
- J’inverse le signe pour trouver
- Dans le cas où alors on recommence le raisonnement avec donc en résolvant l’équation .